
Viewing Coordinate로 좌표변환이 이루어진 3차원 좌표들을 View Plane상으로 Projection 시키게 되는 이 line들을 Projector(Projection Path, Line)들이라 하는데, Perspective Projection은 이 Projector들이 한 점으로 수렴된다.
이 점을 Projection Reference Point (PRP), 또는 Center Of Projection (COP) 이라 한다.
우선, 궁극적으로 구하고 싶은 값은 무엇인가?
Viewing Coordinate의 3차원 임의의 좌표 x, y, z가 prp를 향해 projection되면서 view plane과 만나는 지점인 (x p, y p, z vp)를 구하고 싶은 것이다.
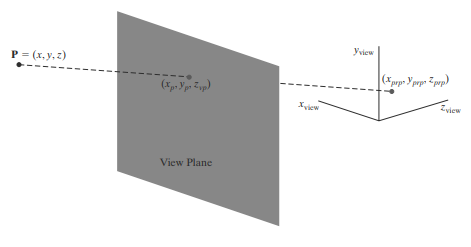
prp의 좌표를 (x prp, y prp, z prp)라 하자.
우린 Viewing Transformation에서 View point (0, 0, 0)를 정했고 이미 알고있다.
[ Q : 그럼 View point는 projection reference point와 같은 것이 아닌가? ]
대부분의 경우에는 같은 것이 맞다. 같을 경우 prp는 (0, 0, 0)이 된다.
하지만 view point와 prp가 무조건 같아야 한다는 보장은 없으며, 다르더라도 이론적, 수학적으로 가능하다.
이 경우, prp가 view plane 반대편으로, 즉 (x, y, z)에 더 가까워 진다면 Synthetic Camera Model처럼 상이 거꾸로 맺히게 된다.
교재에선 view point와 prp가 다른 경우까지 일반화하기 위해 prp를 따로 둔 것.
(x p, y p, z vp)를 구하기 전, z vp는 XY 평면에 평행한 무한한 평면인 view plane의 z 값이므로 이것은 주어진 값, 즉 우리가 알고 있는 값이다.
prp의 좌표 또한 주어진 값, 우리가 알고 있는 값이다.
(x, y, z)와 (x prp, y prp, z prp)를 잇는 projection line내의 좌표를 parametric form으로 나타낼 수 있다.
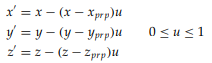
(x', y', z')에서 z'은 z vp인걸 알 수 있고, z vp는 주어진 값, 즉 우리가 알고 있는 값이므로
parametric form의 z성분을 이용해 parameter u를 구할 수 있고, 이는 (x', y', z')를 모두 알 수 있다는 걸 뜻한다.

x, y는 projection될 viewing coordinate의 좌표이므로 알 수 있는 값이고, prp와 z vp는 전부 이미 알고 있는 값이므로 Projection 되는 좌표인 (x p, y p, z p)를 유도해낼 수 있다.
[ 일반화를 벗어난 대부분의 경우 ]
앞서 언급했듯이, prp의 좌표가 임의의점일 경우 일반화를 위한 유도이며, 대부분의 경우 prp가 view point와 같아 (0, 0, 0)이 된다.
이 경우, 아래 식으로 간소화 된다.

[ Perspective Projection View Volume ]

Projection Reference Point를 Apex로 하고 무한히 뻗어나가는 사각 뿔(infinite rectangular pyramid)을 View Volume이라 한다.
pyramid 밖에 있는 모든 Object들은 Clipping Algorithm에 의해 제거된다.
그리고 Projection된 화면이 보이는 곳은 View Plane에 속하는 Clipping Window이다.
무한히 뻗어나간 상태에서 Projection된 Object는 어차피 너무 작아 보이지 않으니 제한을 두기 위해 Far Clipping Plane을 두고, 너무 가까이 있으면 Projection된 Object가 알아볼 수 없을 정도로 크게 보여 제외하기 위해 Near Clipping Plane을 둔다.
Near, Far를 기준으로 View Volume으로 부터 자르고, 이를 View Frustum이라고 한다.
[ Perspective Projection Transformation Matrix ]
이전에 구했던 (x p, y p, z p) 좌표를 Matrix로 나타낼 수 있다.

하지만, 자세히 보면 분모에 ' z '가 포함 되어 있다.
Matrix 내에 오직 상수만 있는 것이 아니라 변수가 포함되므로, z 값에 따라 여러개의 Matrix가 나올 수 있게 된다.
그러므로 하나의 Matrix로 미리 계산해두는 SIMD 연산의 이점을 활용할 수 없게 된다.
이를 해결하기 위해 이전 Geometric Transformations에서 한 번 다뤘었던 homogeneous-coordinate representation이 다시 사용된다.
이전과 다르게 h를 1이 아니라 공통 분모로 갖고 있는 (z prp - z)로 쓴다.
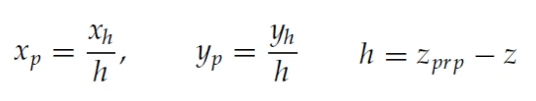
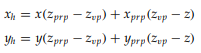
[ Perspective Projection Transformation Matrix using Homogeneous-coordinate representation ]

[ Reference ]
Computer Graphics with OpenGL 4th edition, Hearn, Baker
'컴퓨터공학 > Computer Graphics' 카테고리의 다른 글
| [3D Viewing Pipeline] Perspective Projection - 3 (0) | 2024.07.23 |
|---|---|
| [3D Viewing Pipeline] Perspective Projection - 2 (0) | 2024.07.17 |
| [3D Viewing Pipeline] Viewing Transformation (0) | 2024.07.16 |
| Geometric Transformations (0) | 2024.07.16 |
| Graphics Pipeline Architecture (0) | 2024.07.16 |