[3D Viewing Pipeline] Perspective Projection - 2
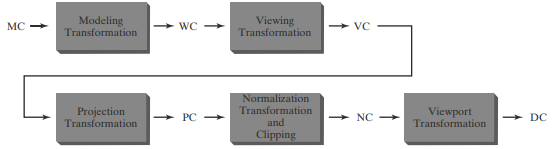
Parallel Projection이 Orthogonal Projection과 Oblique Projection로 나뉘듯이,
Perpective Projection도 Symmetric Perspective Projection Frustum을 갖는 경우와 Asymmetric Perspective Projection Frustum 을 갖는 경우로 나뉜다.
각각 Frustum Centerline이 View Plane에 Perpendicular 한가? 에 따라 나뉜다.
[ [1] Symmetric Perspective Projection Frustum ]

Symmetric Perspective Projection Frustum의 경우,
그러니까 Frustum Centerline이 View Plane에 Perpendicular한 경우, Centerline이 View Plane과 만나는 점은
(x prp, y prp, z vp)가 된다. (수직하므로 prp와 z 좌표만 다르게 되는 것)
이 점을 알게되는 것의 장점은 무엇인가?
Clipping Window의 Width, Height를 세팅하여 준다면 Clipping Window의 네 꼭짓점의 좌표를 구할 수 있다.
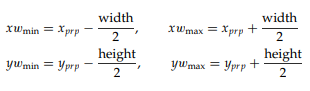
→ Symmetric하다는 특징을 이용해 Clipping Window의 네 좌표를 구할 수 있는 것.
================================================================
Symmetric Perspective Projection을 specify하기 위해 카메라의 property들을 사용하여 다르게 표현할 수도 있다.
- field of view (FOV)
Frustum의 Top과 Bottom 사이의 각을 의미한다.
- aspect ratio (종횡비)
(width / height) of Clipping window
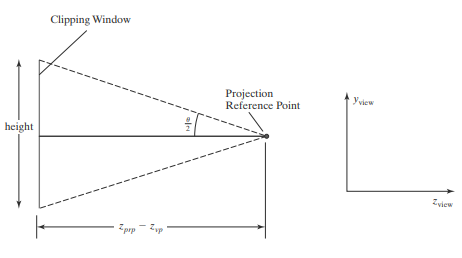

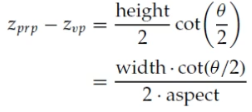
tan(θ/2)를 통해 (z prp - z vp)를 위의 식으로 나타낼 수 있고, Perspective Projection Matrix를 다르게 나타내기 위해 나중에 쓰이게 된다.
================================================================
[ Orthogonal Parallelepiped View Volume ]

Perspective Projection Transformation을 통해, Symmetric Frustum View Volume의 각 좌표는 Clipping Window에 정말로 Projection될까? 다르게 말하면, 각 좌표의 z 는 z vp가 될까? 그렇지는 않다.
실제로 Parallepiped View Volume 형태로 바뀌어 z 값도 갖게 된다. 왜냐하면 Projection이 된 후에도 z 좌표 값들이 필요하기 때문인데, 이에 대해 다음에 더 자세히 다루게 된다.
[ [2] Oblique Perspective Projection Frustum ]

Centerline이 View Plane에 perpendicular 하지 않은 것이 특징이며 Asymmetric Frustum을 가짐. 다르게 말하면, Symmetric와 Asymmetric(Oblique)의 차이는 Centerline이 View Plane에 perpendicular 유무에 따라 나뉘는 것이다.
Oblique Perspective Projection Frustum을 z축에 대한 Shearing Transformation을 통해 Symmetric Frustum으로 변환될 수 있다.
이걸 이용해서 Oblique한 경우의 Perspective Projection Matrix까지 유도해보자.
여기서 2가지 경우를 추가하여 가정한다.
[1] Projection Reference Point가 Viewing-point origin인 경우
(x prp, y prp, z prp) → (0, 0, 0)이 되어 Shearing Transformation은 아래 단순화된 matrix를 가진다.
이제 M (z shear)를 유도해내기 위해 sh zx와 sh zy 성분만 구하면 된다.
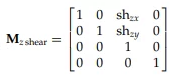
[2] View plane이 near clipping plane에 위치한 경우
Far Clipping Plane은 직접 지정해줘야 하지만, Near Clipping Plane은 View Plane과 같다고 지정할 수도 있다.
여기서는, Asymmetric하기 때문에 Width, Height만으로 Oblique Frustum의 Center of Clipping Window를 구할 수 없다.
그래서 Clipping Window의 네 꼭짓점 좌표의 각 x, y 성분 xw min, xw max, yw min, yw max 이 주어져 있다고 가정해보자.
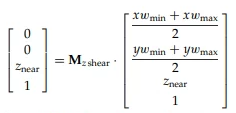
Clipping Window의 Center : ( (xw min + xw max) / 2, (yw min + yw max) / 2 )
Input Matrix에 M (z shear) 연산을 한 결과가 (0, 0, z vp(= z near))라는 것을 통해 M (z shear)의 sh zx, sh zy 성분을 유도해낼 수 있다.

================================================================
[ 음... 그래서 지금 이걸 왜 하고 있는거죠 ? ]
이전 글 [ Perspective Projection - 1 ] 에서, 마지막에 Parametric form을 통해 Perspective Projection Matrix를 1차적으로 유도해냈었다.
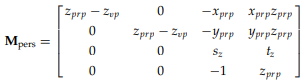
하지만 대부분의 경우, 위에서 가정한 2가지
1) Projection Reference Point가 Viewing coordinate Origin(View Point), 즉 (0, 0, 0) 인 경우
2) Near Clipping Plane이 View Plane인 경우
이 2가지를 가정한다면 Matrix를 간소화 할 수 있다.
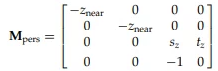
그리고 간소화된 Perspective Projection Matrix에 방금 유도해냈던 M (z shear)을 통해 Oblique Perspective Projection Matrix까지 유도해낼 수 있다.

여태 Oblique Perspective Projection을 유도한 이유는, Symmetric Frustum을 갖는 Perspective Projection까지 포함하여 일반화된 Matrix를 얻을 수 있기 때문이다.
Width, Height가 아니라 xw min, xw max, yw min, yw max로 표현한 이유가 뭘까 ?
위에서 이미 말했지만, Oblique한 경우 기울어져있어 좌우 대칭이 아니기(Asymmetric) 때문이다.
하지만 Oblique Perspective Projection Matrix에서 만약 Symmetric하다면, Near Clipping Plane의 Center 좌표가 (0, 0, z vp)가 되기 때문에 xw min과 xw max의 0을 기준으로한 offset, yw min과 yw max의 0을 기준으로한 offset이 같아진다.
그래서 Matrix에서 (xw min + xw max)와 (yw min + yw max)의 값이 0이 되어 사라지므로 Symmetric한 경우까지 포함한다.
[ Note : 위에서 계속 가정했던 2가지 경우(prp = (0, 0, 0), Near = View Plane)는 현재까지도 가정된 상태다. ]
================================================================
[ Normalized Perspective-Projection Transformation Coordinates ]
Perspective Projection 이후에 Parallelepiped View Volume이 되었고, 이 크기를 2인 Cube 형태로 바꾸는 Normalization이 필요하다.
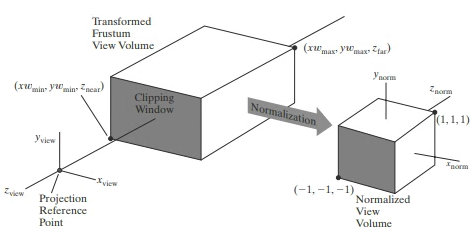
여기서, 오른손 좌표계로 왼손 좌표계로 바뀌게 된다.
다음 단계에서 Device Coordinate로 옮겨가게 되면, 모니터 Screen상에서 모니터 화면으로부터 얼마만큼 들어가 있는가에 해당하는 Depth를 "양수"로 표현하기 위해 왼손 좌표계로 바뀌게 되는 것이다.
Normalization을 위해서, M obliquePers Matrix에 M xy scale 연산을 함으로써 2의 크기로 압축할 수 있다.
xy에 대한 Scaling만 하는 이유는, 앞선 글 [ Perspective Projection - 1 ]에서 Parametric form을 이용한 Perspective Projection Matrix에서 z에 해당하는 Scaling, Translation factor인 s z, t z를 미지수로 처음 두고 현재까지 넘어왔었다.
Perspective Projection에서 z에 해당하는 Scaling, Translation은 어느 값인진 아직 모르지만, 이미 적용되어 넘어왔다고 생각하면 된다.


M obliquepers 에 M xy scale을 한 M normpers 를 구했다.
h를 1로 하는 Homogeneous Coordinate의 임의의 좌표 { x, y, z }에 M normpers를 곱한 좌표를 h를 갖는 Homogeneous Coordinate의 x h, y h, z h로 나타내보자.

그러면 Normalized Perspective Projection된 실제 좌표는 h로 나눈 x p, y p, z p가 된다.
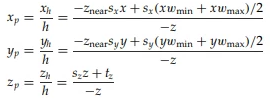
[ Note : 분모(h)가 -z인 이유 ]
앞선 [ Perspective Projection - 1 ]에서 h를 (z prp - z)로 갖는 Homogeneous Coordinate를 사용했었다.
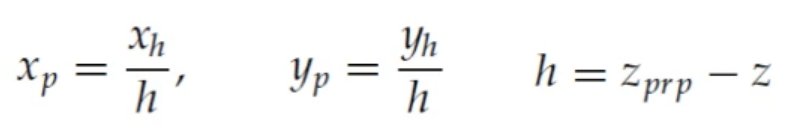
Projection Reference Point가 View Point인 (0, 0, 0)이라고 가정해온 상태기 때문에 h는 (z prp(= 0) - z) : -z가 되는 것이다.
[ Reference : Computer Graphics with OpenGL 4th edition, Hearn, Baker ]