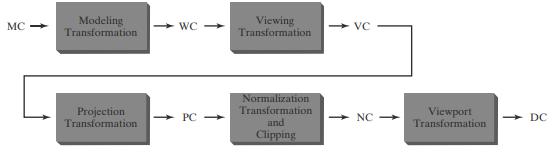
[3D Viewing Pipeline] Viewing Transformation
Object는 본래 자신을 원점으로 하는 Local Space에 존재한다.
World에 배치된다면 World를 기준으로 하는 좌표로 변환되는데, 이걸 Modeling Transformation이라 한다.
R*T에 해당하며 T는 월드의 원점을 기준으로 하는 Translation, R은 좌표축이 맞지않을 때 각각 align하는 Rotation (R(β) R(α)) 이다.
그 다음은, 카메라를 기준으로 하는 좌표계(View Coordinate)로 변경되어야한다. 이걸 Viewing Transformation이라고 한다.
Viewing Transformation이 실행되기전 가장 첫 단계는
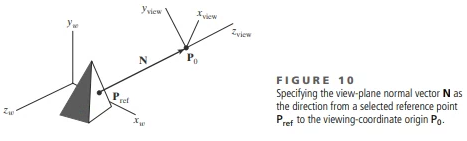
World상에서 주어진 P0 (x0, y0, z0)를 Viewing origin(View point)로 설정한다.
그리고 View plane(Projection Plane)에 수직한 Normal vector인 N을 정해야 하는데,
이는 Approach에 따라 다르다.
1) World의 원점을 향한다고 가정해서 원점과 P0를 통해 N을 구하거나,
2) Reference Point (LookAt)를 설정하여 P(0)와 P(ref) 두 점을 통해 N을 구할 수 있다.
여기서 N을 구한다는 것은 view point의 z축 또한 정해진다는 의미다.
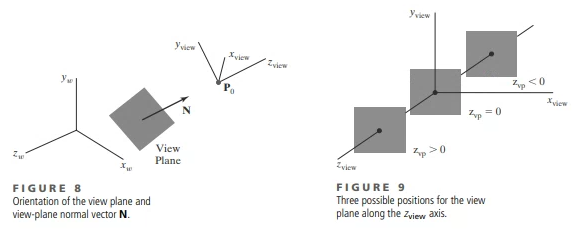
[ Note : Figure 9.를 참고하면, z vp는 view point로 부터 view plane까지 떨어진 스칼라 값을 의미하는데, view point를 기준으로한 z vp의 좌표는 음수가 될 수 밖에 없다 ]
현재까지, view point의 위치와 카메라가 바라보고 있는 점(원점 또는 reference point)을 알고, 이를 통해 view point의 z축 방향과 view plane Normal vector, N까지 알고있다.

다음으로, View point에서 positive y direction을 정하는, 카메라의 위쪽에 해당하는 방향인 View-up vector V를 구해야 한다.
하지만 여기서 N에 perpendicular한 vector는 하나로 정해지는 것이 아니라, 무수히 많아 한번에 정하기 어렵다.
그래서 user-defined orientation이라고 하는 대략적인 V를 정해서 임시로 사용하는데, y축 방향에 가까우면서 간단한 (0, 1, 0)를 사용한다.
N과 V를 cross product하여 x축에 해당하는 vector (N X V)를 얻고, 다시 N과 x축 vector를 cross product하여 y direction을 진짜로 향하는 Adjusted V를 얻게된다.
이로써 view point에서 x, y, z축에 해당하는 vector를 모두 얻게 되었다.
이제 x,y,z vector를 unit vector로 바꿔 편하게 u, v, n 좌표계로 사용해보자.
uvn Viewing-Coordinate

Direct3D의 경우, Left-handed 좌표계를 쓰지만
World 좌표계가 Right-handed 좌표계이기 때문에 Viewing Coordinate도 Right-handed 좌표계인 경우가 더 일반적이며,
OpenGL이 여기에 해당한다.
u, v, n은 모두 unit vector이다.
z axis : view-plane Normal N
y axis : view-up vector V (0, 1, 0), input vector V
x axis : cross product of N and V
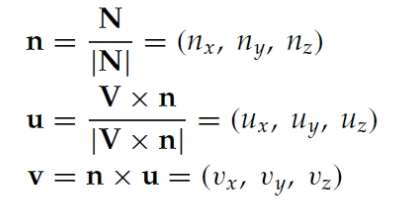
이제 v는 n, u에 수직하며 y direction을 가리키는 진짜 v가 되었다.
[ First Step in 3D viewing pipeline - Transformation from World to Viewing Coordinates ]
Viewing Transformation
1) Viewing coordinate의 원점을 World coordinate의 원점으로 Translation
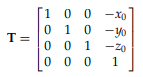
2) view의 x, y, z축을 world의 x, y, z축으로 각각 align하는 Rotation (또는 R(β) R(α))

Viewing Transformation Matrix (World to View)
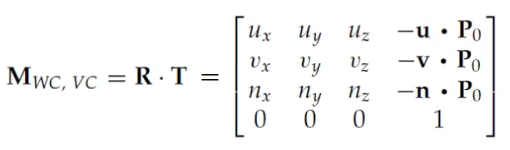
교재에서 Translation factor들(-u*P0, -v*P0, -n*P0)은 다르게 보면 negative Projection의 의미를 갖는다고 나와있다.

현재 Viewing Coordinate까지 옮겨왔으므로 다음으로는 Projection Transformation이 일어날 차례다.
[ Reference ]
Computer Graphics with OpenGL 4th edition, Hearn, Baker