[C++] Merge Sort

[C++] 병합 정렬 (또는 합병 정렬)

 

1945년 폰 노이만에 의해 개발됨.

 

분할 정복 (Divide and Conquer)를 이용한 정렬 알고리즘

분할 (Divide) : 문제를 더 단순하게 분할

정복 (Conquer) 분할된 문제를 해결

결합 (Combine) 결과를 취합하여 마무리

 

 

처음 MergeSort() 내에서, 원소가 1개가 될 때 까지, 즉 경계를 의미하는 left와 right가 같아질 때 까지 재귀적으로 쪼갠다.

1개가 되면, 그 때 부터 개별적으로 정렬한 뒤, 원래 배열에 정렬된 부분을 넣으며 합친다.

 

 

절반 씩 쪼갤 때 O(log N), 다시 합칠 때 총 N개를 합치므로 O(N)으로 총 O(N log N)의 시간 복잡도를 가진다.

그러므로 최선, 평균, 최악의 시간 복잡도 O(N log N)을 가진다.

 

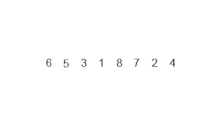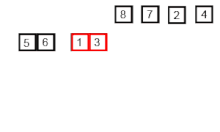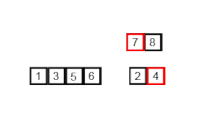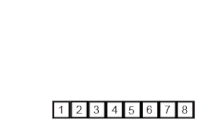
[ 구현 연습 ]

/*
*  Merge Sort
*  Divide and Conquer
*/
 
void MergeResult(vector<int>& v, int left, int mid, int right)
{
    int leftIdx = left;
    int rightIdx = mid + 1;
 
    vector<int> temp;
 
    while (leftIdx <= mid && rightIdx <= right)
    {
        if (v[leftIdx] <= v[rightIdx])
        {
            temp.push_back(v[leftIdx]);
            leftIdx++;
        }
        else
        {
            temp.push_back(v[rightIdx]);
            rightIdx++;
        }
    }
 
    // 왼쪽이 먼저 끝났으면, 오른쪽 나머지 데이터 복사
    if (leftIdx > mid)
    {
        while (rightIdx <= right)
        {
            temp.push_back(v[rightIdx]);
            rightIdx++;
        }
    }
    else // 오른쪽이 먼저 끝났으면, 왼쪽 나머지 데이터 복사
    {
        while (leftIdx <= mid)
        {
            temp.push_back(v[leftIdx]);
            leftIdx++;
        }
    }
 
    for (int i = 0; i < temp.size(); i++)
        v[left + i] = temp[i];
}
 
void MergeSort(vector<int>& v, int left, int right)
{
    // base case
    if (left >= right)
        return;
    
    int mid = (left + right) / 2;
    MergeSort(v, left, mid);
    MergeSort(v, mid + 1, right);
 
    MergeResult(v, left, mid, right);
}
 
int main(void)
{
    ios_base::sync_with_stdio(false);
    cin.tie(0);
     
    vector<int> v;
 
    srand(time(0));
 
    for (int i = 0; i < 50; i++)
    {
        v.push_back(rand() % 50);
    }
 
    MergeSort(v, 0, v.size() - 1);
 
    for (const int i : v)
    {
        cout << i << "\n";
    }
 
    return 0;
}

[ 결과 ]

50개의 랜덤한 값 정렬

 

 

 

 

 

 

[ Reference : Rookiss의 C++ Part3 자료구조 ]